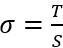CUESTIÓN Nº1
La siguiente tabla muestra los valores
registrados durante un ensayo de tracción sobre una probeta de 100 mm de
longitud y 20 mm de diámetro:
Tension (MPa) 0 135
150 135 150 165
Elongación 0 4·10-3
6·10-3 10·10-3 16·10-3 20·10-3
a) Represente gráficamente el diagrama
de tensión - elongación.
b) Enuncie la Ley de Hooke y calcule el
módulo de elasticidad del material.
La ley de Hooke establece
que en la zona elástica la tensión y la elongación son proporcionales, la
constante de proporcionalidad recibe el nombre de módulo de Young ó módulo de
elasticidad
Por tanto para calcular el
Módulo de Young nos hemos de asegurar que estamos en la zona elástica. Si nos
fijamos en la gráfica el único punto que podemos tomar es con la tensión a 135
Mpa y la elongación a 4·10-3
En ese caso E= 33750MPa
c) Calcule la fuerza aplicada
para someter la probeta a una tensión de 80 MPa y la elongación que
sufrirá.
Teniendo en cuenta que S=
3,14·10-4 m F=σ·S= 25120N
y a partir de la expresión del módulo de Young ε=2,37·10-3
d)Calcule el incremento de longitud que
alcanza la probeta para la tensión de 80 MPa ¿Recuperaría la probeta sus
dimensiones si cesara la tensión en ese momento?


podemos ver en la gráfica que estamos dentro de la zona elástica por tanto, recuperará sus dimensiones
CUESTIÓN Nº2
Se
ha sometido una probeta de sección cuadrada de lado 2 cm y longitud 25 cm a un
ensayo de tracción, sufriendo un alargamiento de 2,5·10-3 cm al
aplicar una carga de 10.000 N. Teniendo en cuenta que el material muestra un
comportamiento elástico y que su tensión de rotura es de 130 MPa, determine:
a) La tensión y la deformación unitaria al aplicar la carga.
T=10000N S=4·10-4
m2 σ=25MPa
Δl=2,5·10-5m l0=
0,25m ε=10-4m
b)
El módulo de Young del material.
E= 250·103 MPa
c) La carga máxima que
admite la pieza para que la deformación unitaria no pase de 5·10-4.
σ=125MPa y
T=50KN, podemos ver que no sobrepasamos
la tensión de rotura
Cuestión nº 3
Una probeta de acero de 30 mm de diámetro y 250 mm de longitud entre puntos calibrados está siendo sometida a un esfuerzo de tracción de 6000 Kg e incrementa su longitud en 0,20 mm. Calcula la tensión unitaria, el alargamiento unitario y el módulo de elasticidad.