Para trabajar con corriente alterna utilizaremos la notación compleja, recordemos los conceptos básicos que ya habéis visto en matemáticas
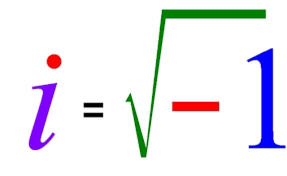
un nº complejo consta de una parte real y una parte imaginaria
en corriente alterna en lugar de utilizar i como unidad imaginaria utilizaremos j, para evitar la confusión con la variable intensidad.
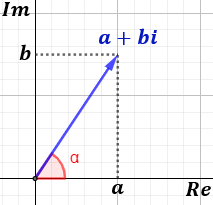
Los números complejos se representan en un plano complejo, de modo que la parte real se represente en el eje de abscisas, llamado EJE REAL, y la parte imaginaria en el eje de ordenadas, llamado EJE IMAGINARIO.
Existen diferentes formas de expresar un nº complejo.
El complejo z se representa como el vector con coordenadas(a,b), esta representación se conoce como forma binómica o rectangular y la utilizaremos en sumas y restas

La longitud del vector se denomina módulo del complejo z . El ángulo que forma el vector con la parte positiva del eje real se denomina argumento del complejo z: por tanto podemos expresar el nº complejo de la forma
Z=rα
que se conoce como forma polar y la utilizaremos para realizar productos y cocientes.
Ambas representaciones están relacionadas
En cálculos de corriente alterna necesitamos constantemente pasar de rectangulares a polares y de polares a rectangulares, por ello debemos aprovechar la función de la calculadora que nos permite este paso. Aunque cada modelo es diferente esta función aparece en general en Pol (para pasar a polares) y Rec (para pasar a rectangulares)
